行测必迈的坎：排列组合
[??
未知
??]
作者：
2018-07-09 17:43:01
|
在行测科目中，排列组合题目既是重点也是难点。由于它与生活联系密切、题型相对灵活、解题难度大，对于没有任何基础的考生而言，掌握起来并非易事。下面小编带大家来学习排列组合中涉及的解题方法，碰到难题也能迎刃而解。
一、优限法
所谓优限法就是，在解决排列组合问题时，对于有限制性条件的元素优先安排。
例：世界杯来临，替补席有一排七个座位供七个替补队员就坐。其中，有两名运动员执意要坐两端，总共有多少种安排方式?
解析：先排位置有限制要求的两名球员，有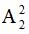
种排法，剩余的球员有
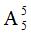种排法。根据分步相乘的原则，最终安排方式有
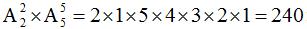种。
种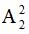排法，剩余的球员有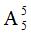种排法。根据分步相乘的原则，最终安排方式有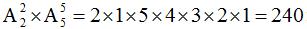种。
二、捆绑法
所谓捆绑法就是，在解决排列组合问题时，先将相邻元素放在一起，内部进行排列组合，看成一个整体。然后把这个整体看成一个元素，和其他剩余的元素再放在一起进行排列组合。
例：世界杯来临，替补席有一排七个座位供七个替补队员就坐。其中，有三名三十岁以上的运动员执意要坐在一起，总共有多少种安排方式?
解析：先将三名要求在一起的放在一起进行排列，有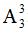
种方法。然后把它当成一个整体和其他四个元素放在一起进行排列有
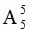种方式。根据分布相乘的原则，最终安排方式共有
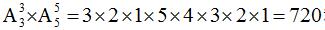种方法。
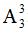种方法。然后把它当成一个整体和其他四个元素放在一起进行排列有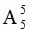种方式。根据分布相乘的原则，最终安排方式共有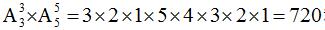种方法。
三、插空法
所谓的插空法就是，当有元素要求不相邻时，先排其他元素，再将指定的不相邻的元素插入他们的空隙或者两端。
例：世界杯来临，替补席有一排七个座位供七个替补队员就坐。其中，有三名三十岁以上的运动员彼此不相邻，总共有多少种安排方式?
解析：先将没说不相邻的四名要求在一起的放在一起进行排列，有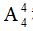 
种方法。然后，这四个元素的位置确定后，把剩下的明确不相邻的元素放在指定的五个空里，有
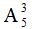种方式。根据分布相乘的原则，最终安排方式共有
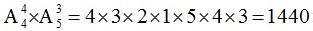种方法。
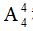种方法。然后，这四个元素的位置确定后，把剩下的明确不相邻的元素放在指定的五个空里，有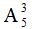种方式。根据分布相乘的原则，最终安排方式共有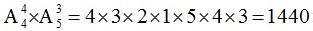种方法。
和排列组合一样，行测中的每类题型都有自己的一套复习方法和策略。得其道，势必事半功倍。悟其法，方能赢国考。最后，祝您备考成功，顺利通过考试!
责任编辑：大晴子
浏览次数： 次